How to turn linear phase into truly linear phase

In the previous episode, I pointed out the perils of phase-flipping in the stopband of FIR filters. Now here are various ways of fixing this.

We saw last time that FIR filters can have phase jumps in the stopband that might affect some signals in some cases. We need something in our toolbox to mitigate this. Fortunately there are several approaches we can take.

There’s a simple brute-force approach. Since using one of these filters on your signal causes occasional unwanted phase flips by pi radians, using two in series must cause phase jumps of 2pi radians. That’s the same as no phase jump at all! Though sometimes the plot will still show a jump of 2pi, depending on the plot routines used – now only a cosmetic rather than processing issue, but still a little annoying.

The downside is that we almost (one less than – can you see why?) double the number of coefficients in our filter, which might not suit your hardware. We also significantly change the filter response, of course. There will be twice the dB level of droop or ripple in the passband (which might now be unacceptable) and twice the dB stopband attenuation (good, probably, but maybe now over-engineered).

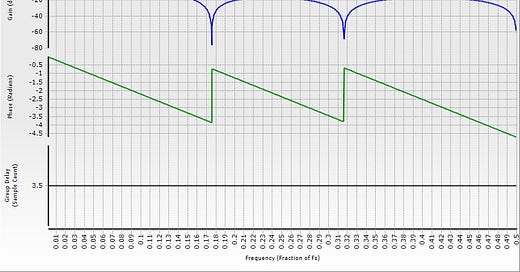
Figure 1 shows an example filter. This time, I used a third-party filter design program, FIRBBC, to create the coefficients for a small 8-tap equiripple filter.

Figure 1: An 8-tap equiripple lowpass filter with stopband phase jumps.

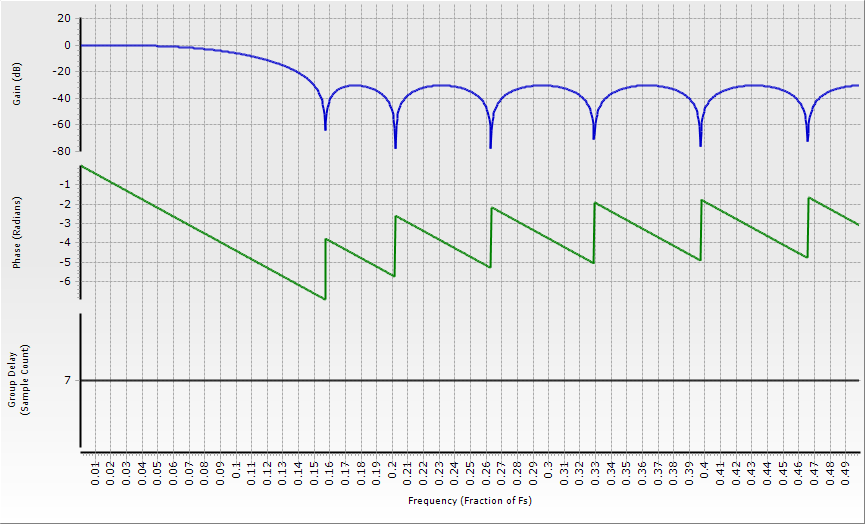
If we cascade two of the figure 1 filters, we get a 15-tap filter (figure 2) that has twice the passband droop, twice the stopband attenuation – and no stopband phase jumps!

Figure 2: Cascading two of figure 1’s filters gets rid of the stopband phase jumps.

Another approach is to manipulate the FIR filter’s impulse response directly to eliminate the jumps. One never gets something for nothing, so let’s look at the tradeoff we might have to make. As we saw last time, all filters with this rogue phase issue have one thing in common: the Fourier transform of the impulse response (basically the frequency response, but this is a nice way to think about it in linear terms) has some regions in which its value is negative. In the case of filters with many taps, there can be many such regions.

We can fix that, though. Consider the Fourier transform of a pulse that has a non-zero height only for a single sample. It has a constant magnitude for every frequency component, and a delay that depends on the time at which it occurs. So, what we can do is ‘tweak’ the impulse response of our ‘jumpy’ filter by adding a little bit of single-sample pulse to it, just enough amplitude, and in the right place, so that the positive components cancel out the negative parts of the Fourier transform. It should be fairly obvious that we should add this pulse right at the center of symmetry of the impulse response, so this technique is much simpler to apply in the case of an odd number of taps, where the group delay is equal to the time at which the center coefficient appears.

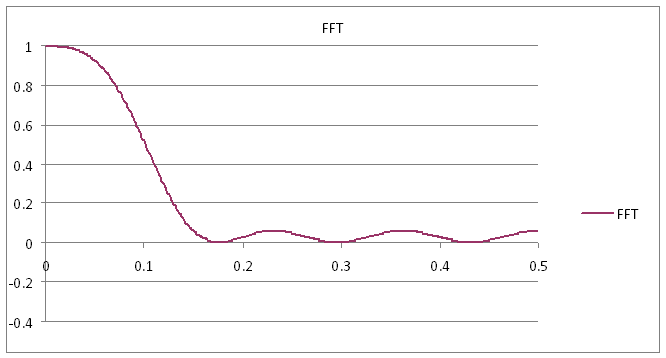
How much of this sample do we have to add? Well, let’s look at another example. I used FIRBBC to design a 15-tap filter, shown in figure 3. It has an equiripple stopband with plenty of stopband nulls and plenty of pi phase jumps. Figure 4 shows the amplitude of the Fourier transform of the coefficient series, correcting for the signal delay through the filter. Strictly, it’s an FFT (in Excel!) of the 15 taps padded out to 1024 samples with zeroes. It shows clearly where the Fourier transform goes negative.

Figure 3: A 15-tap equiripple lowpass filter.

Figure 4: Fourier transform of the coefficients used to produce the filter in figure 3.

Closer inspection of the filter’s stopband shows that it rises up to -30.34 dB, which corresponds to a linear value of 0.0304. The largest coefficient value of the filter is 0.1952 so we increase just this coefficient to 0.2256 by adding the 0.0304. This is imperceptible when you just look at the impulse or step response. When we now plot the overall Fourier transform we find that it doesn’t go negative, see figure 5. And when we plot the response of the filter, the phase jaggies are gone! The group delay is unchanged.

Figure 5: 15-tap filter, center coefficient modified for non-negative Fourier transform.

Figure 6: The responses of the Fourier-modified 15-tap filter.

The eagle-eyed will notice that the stopband rejection has deteriorated a little. That’s to be expected. We added enough signal at every frequency to cancel out the most-negative portions of the Fourier transform. In those stopband regions where the response is already non-inverting, but with the same magnitude as the most negative parts, we might therefore as much as double the signal level. So, when using this technique, over-design your stopband by 6 dB, to allow for this reduction.

By the way, this additive technique is also deployed as a step in a different task, which is to create minimum phase FIR filters. That’s for another time.

The technique also ‘works’ for the simple 7-day averager case shown last time. By changing the center coefficient value from 0.14286 to 0.37593 and adjusting the gain to get back 0 dB at DC, we get no ‘jaggies’(figure 7) and therefore no inversion in the stopband (figure 8).

Figure 7: The seven-day averager tweaked to eliminate the stopband inversion.

Now we can see in figure 8 that the six-day response is no longer inverted (compare this to figure 3 in “How linear-phase filters can still cause phase distortion”.

Figure 8: Time response of the tweaked averager to the six-day fluctuation.

If you start with a filter that has a half-decent stopband – which should mean in the majority of cases, if you’re serious about your filtering – this isn’t going to make that much difference to the signals passing through. But by eliminating this source of indeterminacy in the spectrum of your signal, you may find that analyses relying on Fourier transforms don’t fall over so much due to discontinuities in sign. Why don’t you try this out and let me know if you have an application where it makes a difference? Don’t let your filter give you that old excuse: “it’s just a phase I’m going through…”