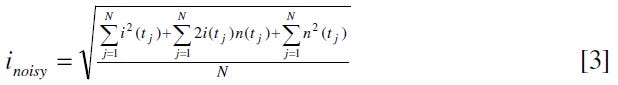Measurement noise: when 1000*1000 isn't a million
(Darn. Kind of given the game away)
Let’s say you have an AC current measuring channel that adds a little noise. How does this affect the accuracy of your current measurement? What does the dynamic range of the channel need to be in order to deliver a certain accuracy?
To take a specific case, let’s suppose that, when measuring a current that is 60 dB down on the system’s full-scale capability – in other words, one-thousandth of the full-scale signal. Let’s suppose that you want the accuracy impact of the presence of channel noise to be no more than 0.1%. Again, one part in a thousand.
A superficial analysis might say that if you need one part in a thousand uncertainty on a signal that’s one-thousandth of your full scale, you need a dynamic range of 1000*1000 or a million, which is 120 dB.
That’s not easy! But is that thumbnail analysis correct? Let’s do some sums.
By definition, the RMS value of a current i(t) over a measurement interval of N samples is:
and, for a noisy current which is the ideal current plus a noise signal n(t):
We can multiply out the square of the two currents in [2]:
and recognize that, since i(t) and n(t) are uncorrelated, the integral (or sum) of their product tends to zero for large enough N, so we can strike out that term, resulting in:
And, manipulating [4]:
But the (rms) signal-to-noise ratio snr is just
by definition, and we can substitute [6] into the RHS of [5]:
and solve this for snr to get the following expression:
Practical Example
For our 0.1% accuracy case at a current which is 0.1% of full scale, this implies inoisy/irms =1.001 and substituting this into [8], we have
and this is relative to a signal level of -60 dB, so the required dB snr referred to full scale is (60 dB+27 dB) = 87 dB.
This is way more encouraging than 120 dB and is within the reach of many embedded MCU ADCs.