My 1986 exploration of subtractive crossovers 'done my way'
based on the Vanderkooy & Lipschitz paper
As I mentioned in the previous post, I was quite inspired by the Vanderkooy & Lipschitz paper I’ve referenced. That paper showed some examples of deriving a highpass crossover function by subtracting a suitable lowpass function from a pure time delay. Naturally when you add the derived highpass and the original lowpass filter, you get back a perfect time delay. That’s probably about the lowest level of insult you can apply to an audio signal.
The reason that was a big deal is that, in conventional crossover design, when you add together the lowpass and the highpass functions you’ve chosen, you generally don’t get the original signal just delayed by some period of time. Even if the on-axis magnitude response of the summed crossover lowpass and highpass filters is ruler-flat over frequency, the phase shift with respect to the input does not have the characteristics of a pure time delay. It has the behaviour of an all-pass filter, whose phase shift is not purely proportional to frequency, but has some other behavior.
The question has always been: is that behavior harmful in some way to music reproduction? People have agonized about this for decades. It’s certainly the case that when you use our standard blunt instrument for testing system response, the squarewave, what comes out as the summation can often look entirely different from what went in. It’s natural to ask whether the dramatic visual impact on an oscilloscope translates to any kind of impact on our ear-brain combo, at least for some varieties of signal.
(Actually, of course, our bluntest instrument is the sinewave. The squarewave is only the second bluntest instrument).
The IEEE paper I reference in the previous piece - which I had not seen until Charlie Laub referenced it in his latest AudioXpress piece - focused on a fairly forensic way of doing some listening tests to determine our propensity to detect variations in midband group delay. It’s nice work, though I have a small reservation about it. That is, that the testing was not done on actual examples of the overall shape of the group delay curve you get from such crossover summations, if you are doing them the old-fashioned way without a lot of digital post-processing. If you have that kind of processing available, you should be able to correct for everything, so I think the test design was rather artificial. Still, they point in broadly the same direction - on some signals, to some people, some small sub-millisecond undulations in group delay are audible.
Now wind the clock back to the mid-80s, before fancy DSP was widely available to the audio system designer. In fact, in the speakers I envisaged designing at the time, I wasn’t going to be using any digital processing at all - not even simple digitally-based signal delay. So I wanted to explore a pure analog way - active, of course, since that was all the rage then.
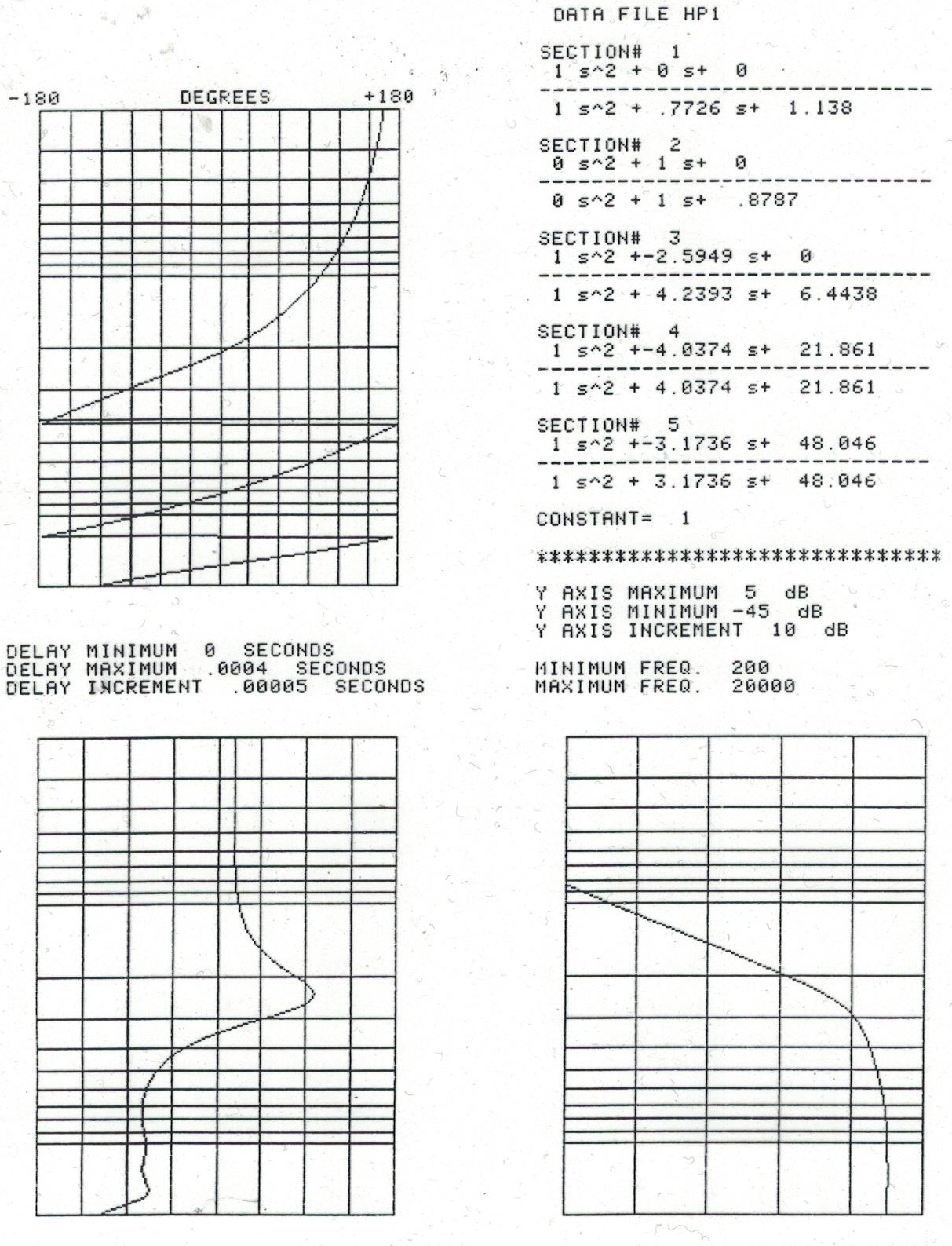
This is how my thinking went. If I add conventional HP and LP crossover paths together, I’ll get an allpass response, possibly with quite significant impact on group delay and waveform reproduction. If only I could make the V&L subtractive HP filter, I’d be much closer to this ‘ideal’ of zero insult on the signal. Now, I can’t make a pure delay with analog filters 0 but I can get quite close. I can design a higher order allpass filter whose delay is acceptably constant right up to a reasonable upper limiting frequency, much further away from all the important frequency components of what we’re interested in. Then I can subtract a candidate LP filter from that, and get something close to the response that V&L show in their paper.
Component tolerances might conspire to make this troublesome in production - we don’t want to have to use unobtanium levels of accuracy and tolerance. But now there’s something I can do. Because I can express the transfer function of my planned allpass filter in exactly the same format as that of the LP filter. So I can do the subtraction algebraically, to get the required transfer function of the HP filter, and then implement that directly!
And that, dear readers, is what I did. And, what’s more, the evidence of this very early work is still there on the Web:
https://www.ioa.org.uk/catalogue/paper/developments-linear-phase-crossover-design
That scan of the Conference Digest doesn’t have the images that I showed on the overhead when I presented it back in 1986 - but a few years back I found those acetates, photocopied from the thermal printouts of the HP-85 on which I had done the work!
In the third set of plots, you can see a comparison between a standard Linkwitz-Riley 4th order combo (top panel) and the new filters (bottom panel). You can easily see that when the lowpass wobbles up, the highpass wobbles down, for the new filters, but not at all for the L-R.
The ‘ringing’, by the way, is because these squarewave responses were done the canonical way, by summing harmonics up to an upper limit (I might have been thinking 48 kHz because I had been working on early digital audio mixing desk electronics - that’s for another post!)
When I get a moment I’ll drop these transfer functions into some much more modern simulations. After I’d published this, I did a little more work on power response, and these filters do come put pretty nicely there too.
All from the way way back machine for the moment! — K



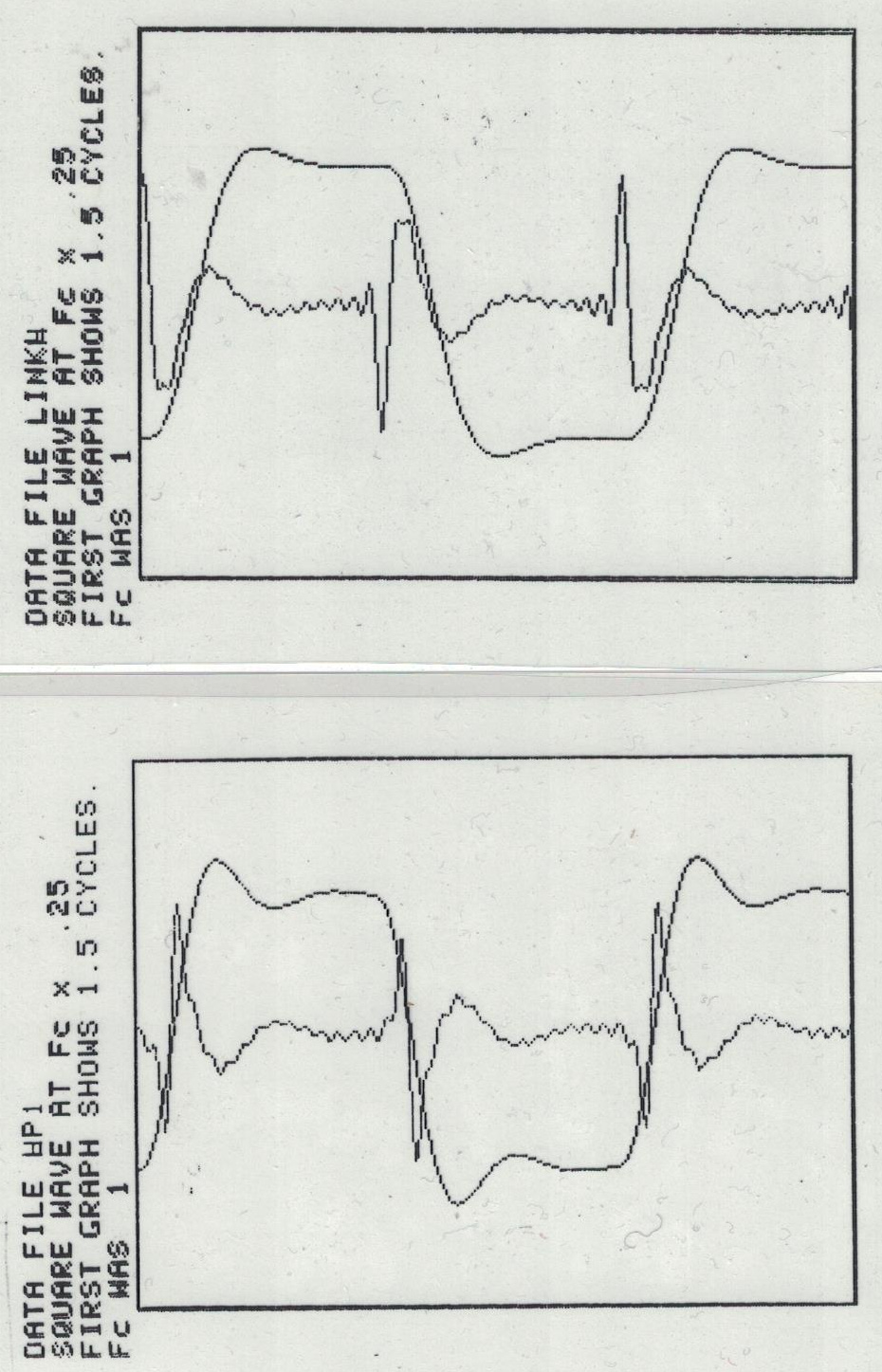
So those spikes and ripples on the square wave are just the missing terms above 48kHz? I've often thought how ironic this is, that you filter something and it comes out less smooth, not to mention the overshoot always staying the same magnitude. (I can't remember the name of that effect though I was talking about it just a few months ago. Urgh! 😏)
I have to say that I have managed to find near zero correlation between time coherence and sound quality and these days you are unlikely to find an actual Bessel filter in anything I'm working on. I remember you always saying how soggy they were and how they didn't really do very much actual filtering. I now have exactly that view and almost marvel at how little they do. Even in pre amps, what was my 70kHz final 3rd Order Bessel filter has been replaced by a 100kHz 3rd Order Butterworth which is almost indistinguishable for phase linearity but does more filtering and doesn't encroach into the passband nearly as badly. In speakers it's all odd-order Butterworths, at least as a framework. I would say keeping the power response flat (and there's more to this than just the Butterworth summing) is vastly more important and contributes to the sense of timing more than any linear phase-ish shape. I also think it's important to have the two responses in quadrature so that the outputs don't interfere with each other and a L-R definitely doesn't provide that.
Designing any of these listening tests is fraught with scope for misinterpretation. Even Floyd Toole's work on dispersion is flawed by so many other things being affected by moving the crossover frequency. I'm in agreement with him that keeping discontinuities out of the dispersion characteristics is important but we're never going to know whether what his listening panel liked was lower distortion from the mid-bass (being mostly below breakup), less chance for it to beam certain frequencies at you, or missing out contributions from the dust cap (which often produces a last dying peak at around 5k).
I think the use of Bessels in crossovers did bring a benefit but it was more one of competent design. So many speakers pre- the Personal Computer, and especially outside the competent manufacturers, were just plain flawed, with actual design mistakes in them. The Bessel couldn't be knocked up on a pocket calculator quite as easily and obviously as a 2nd Order Butterworth and if it was, it was so heavily damped that changes in component values hardly made a difference - and you certainly didn't get any surprises. But I'm yet to be convinced that it actually brought any positives because of its linear phase nature.
I'm a bit puzzled as to how the L-R is performing quite decently on the power response front since it's one of the very worst for that with its notch at crossover. For me it gives that ultimate "domestic sound" with the band members trotting across the top of your mantlepiece and never being able to muster up any sense of scale or power. Guess i'll have to wait for your next piece. :)