Response-Compensated Equalizer Design part 4: Yes, it’s the code
This final part includes C code for the functions used to implement my “wow, the response goes through all the sliders!” compensation scheme – ExactFit.
The algorithms were initially developed in BBC Basic for Windows (my favorite development tool) and then translated into C (well, I needed the practice). The C files were compiled with GCC to a DLL that can be called from any suitable program. I used a BBC Basic for Windows shell program for my own testing and validation purposes.
To meet schedule and performance requirements in the demo for a Fruit Company conference, the C code was embedded within an iPhone App (written in ObjectiveC by a subcontractor) which provides the human interface and control layer.
Input to the ExactFit algorithm
The raw input to the algorithm is a vector or array of desired gain points defined at the band center frequencies implemented in the equalizer. The reference design is a ten-band equalizer, but the method scales to any number of bands. The bands do not need to be regularly spaced (though the algorithms have not yet been tested in the general paragraphic case).
It is customary to define the desired frequency response on a dB scale. The algorithms can be configured with a calling parameter to interpret the incoming gain as a ‘sqrg’ figure instead, that is, the square root of the required gain. That is an efficient format for communicating with the equalizer, as mentioned in Part 3.
In a system using floating point arithmetic, there’s no particular need to limit the resolution of the desired gain values, though it doesn’t make much sense to specify them with any greater precision than is implied by the tolerable accuracy of the result of the compensation or its measurement on a frequency response analyzer. With the typical settings used in the algorithms here, the frequency response has never been found to be more than 0.03 dB out from the demanded value even on ‘pathological’ cases. Typical accuracy is much better than ±0.01 dB. The algorithms have been tested on both double and single precision floating point arithmetic, using the Numerical Recipes machar() function to ensure that the compiler switches were forcing the precision correctly.
Output from the ExactFit algorithm
The desired result of running this algorithm is a vector of set gain points used by the filter coefficient calculation routine. These can be expressed in dB form for plotting, or in ‘sqrg’ format for onward transmission to the equalizer hardware (a communication protocol was also defined for this work but the details are proprietary to the Fruit Company).
Input to the BestGain algorithm
The BestGain algorithm takes a vector of dB gain values. No format parameter is passed in the function call; the function was designed only to take dB and not the ‘sqrg’ format used by the equalizer hardware. That’s because the BestGain function is applied prior to the ExactFit algorithm and is never used to communicate directly with the equalizer hardware. The ExactFit feature can be bypassed; if this is achieved by simply not calling the exact_fit() function, then the dB gain value needs to be converted to sqrg format with the following code fragment (or its equivalent):
for (i=0; i<=ncf; i++) {
sqrg[i] = (double) pow(10.0, dBgain[i]/40.0);
}The BestGain function sometimes makes no changes to the gain array; this is the case either when the correction would be less than 1 dB, or when a majority of the demanded gains are the same to within 1 dB. So, for instance, on a 10-band equalizer, moving up to four of the sliders to arbitrary new positions will not result in any change to the gain offset demanded by best_gain().
Structure of an application using these functions
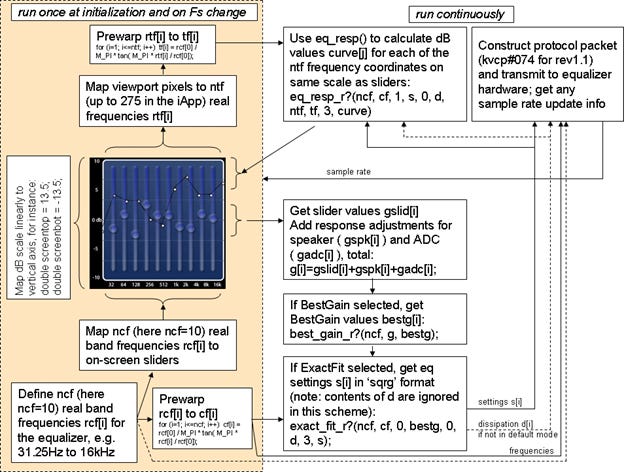
A flowchart of a suitable control application is shown in figure 1. The graphical user interface is assumed to map frequency in logarithmic form onto the horizontal axis of the screen, and gain in dB onto the vertical axis. The equalizer algorithms don’t include the system-specific and generally trivial linear transformations between gain and frequency, and the user drawing units or pixel coordinates used to reference screen locations.
Figure 1: an outline of the overall system
This application may be used in a system with an inherently non-flat frequency response that needs to be compensated along with the desired user frequency response. For instance, the non-flat frequency response of audio converters can be accommodated. A frequency response correction vector can also be applied. When equalizing a loudspeaker assembly, the octave-averaged frequency response is sampled at the band center frequency to provide a basis for equalization. Slider movements are then additive to this pre-equalized response. Frequencies can be passed to the protocol either as ‘real world’ or prewarped values.
The ExactFit algorithm is configured to deliver results directly in the format needed to fill the protocol payload. These results can also be read directly by the eq_resp() function that produces the necessary data for the frequency response plot. Note that if double precision arithmetic is chosen for the algorithms, then a format conversion will be needed to generate the data for the protocol block, which has been specified to take single precision, four-byte floats.
All the arrays used in the functions are unit-offset as far as the frequencies are concerned. The 0th element of each array is used for auxiliary data. The 0th element of the frequency arrays contain the sample rate being used by the application (that therefore needs to be known, i.e. returned by the hardware if it can be changed outside the application’s control). The 0th element of the gain array contains the flat gain that the equalizer must implement in addition to all the variable responses. This is used in a hardware-specific way; these algorithms do not assert whether this gain should be pre-, post- or mid-filter. The 0th element of the dissipation array returns the iteration count from the algorithm in exact_fit() and this can be snooped for diagnostic purposes. At the time of writing, the dissipation array is not used by the equalizer hardware, and the dfmt parameter must consistently be set to zero for all functions.
Use of the C functions
These descriptions are for the versions of the functions delivered in the first exploratory release.
For testing purposes on a PC, the functions are compiled (with GCC) into a DLL so that the routines can be called by a code test jig for verification. This is the purpose of the #definition of EXPORT. This is not needed in a stand-alone application. The code is written to ANSI C guidelines.
void exact_fit_r2(int ncf, double *cf, int gfmt, double *g, int dfmt, double *d, int sretfmt, double *s)
This is the main ExactFit optimization routine. In the base usage case, it takes an array of gain values g[] which is usually in dB but can be in ‘sqrg’ format if gfmt>0. It also takes an array of band center frequencies cf[] that have been prewarped by a simple routine, and can be either native or scaled by any factor (i.e. pi/Fs), since the routine is only sensitive to the ratio between adjacent frequencies. It returns in s[] an array of setting values for the equalizer hardware, which can either be in dB, or in the ‘sqrg’ format that is actually sent to the equalizer hardware, if sretfmt==0.
The array s[] is also used to provide a starting value for the approximation. When the routine is first run, the input array g[] can be used to ‘seed’ the algorithm. In fact, the choice of s[] is not critical, and seeding with an all-zero array produces results just as quickly. Subsequently, the function is seeded by the previous settings, and if the array s[] is static within the calling context, nothing needs to be done at all. If not, then s[] needs to be set to contain the current value of settings. For any single-slider move, the algorithm is likely to converge in a single step, making incremental updates very rapid.
Optionally, the default dissipation values can overridden by values calculated from information sent in d[] when dfmt>0. This would be done to deploy the system as a paragraphic equalizer, or to use more sophisticated schemes for optimizing the filter dissipation values. For instance, an additional layer of optimization may be able to improve the fit of the realized response between the defined bands by careful re-adjustment of the filter dissipation values. This may be useful in active speaker applications, where more response fine-tuning may be possible.
ExactFit contains an iteration loop that terminates when the settings values change by less than a certain amount from one iteration to the next. The actual response is not checked during the iteration. This prevents the algorithm from terminating on a pathological false solution that meets a response-matching criterion. The way in which the system’s characteristic equations are derived ensures that the algorithm will converge, that is, each successive calculation of a candidate array of settings is closer to the ‘correct’ value.
All the routines printed here declare their floating point variables as double precision. If single precision arithmetic is required to speed things up, then declarations of type ‘double’ are replaced with type ‘float’. Single precision versions of math functions and memory allocation must also be used in that case, along with compiler switches that ensure that single precision arithmetic is actually used. The algorithms have been tested with both single- and double-precision IEEE754 floating point arithmetic, and the differences in convergence and accuracy are small enough to be neglected completely.
#define EXPORT __declspec(dllexport)
#include <math.h>
#include "nrutil.h"
#include "eq_resp_r4.h"
#include "klusolve.h"
EXPORT
void exact_fit_r2(int ncf, double *cf, int gfmt, double *g, int dfmt, double *d, int sretfmt, double *s)
{
/* note: the ncf passed here is the actual number of center frequency bands */
/* note that the seed value to first call of eq_resp is assumed to be in gfmt format! */
double teststop = 0.1;
double *gtemp, *nrig;
double **result;
int i,j;
int converged;
/* choose vector(), matrix() for single precision; dvector(), dmatrix() for double precision */
gtemp = dvector(0,ncf);
nrig = dvector(0,ncf);
result = dmatrix(0,ncf,0,ncf);
/* first get a starting result array */
eq_resp_r4(ncf, cf, gfmt, s, dfmt, d, ncf, cf, 1, result);
/* then get a starting solution vector; can re-use s */
for (i=0; i<=ncf; i++) {
nrig[i]=g[i];
}
klusolve(result, ncf, nrig);
/* starting solution now in nrig */
j=0;
converged = 0;
while(converged==0) {
/* save previous value in gtemp */
for (i=1; i<=ncf; i++) {
gtemp[i]=nrig[i];
nrig[i]=g[i];
}
/* get next approximation */
eq_resp_r4(ncf, cf, gfmt, gtemp, dfmt, d, ncf, cf, 1, result);
klusolve(result, ncf, nrig);
/* now s has next approximation in it */
j++;
converged = 1;
for (i=1;i<=ncf && converged==1; i++) {
if (fabs(nrig[i]-gtemp[i]) > teststop) {
converged = 0;
}
}
/* now converged=0 if we need to go round again, else nrig has correct value */
}
/* if sretfmt=0, just return, because we're done, else return sqrg */
if (sretfmt > 0) {
for (i=0; i<=ncf; i++) {
s[i] = (double) pow(10.0,nrig[i]/40.0);
}
}
else {
for (i=0; i<=ncf; i++) {
s[i] = nrig[i];
}
}
d[0] = (double) j * 1.0;
/* choose free_vector(), free_matrix() for single precision; free_dvector(), free_dmatrix() for double precision */
free_dvector(gtemp,0,ncf);
free_dvector(nrig,0,ncf);
free_dmatrix(result,0,ncf,0,ncf);
}void eq_resp_r4(int ncf, double *cf, int gfmt, double *g, int dfmt, double *d, int ntf, double *tf, int rfmt, double **result)
This routine works out the response of all the equalizer filter bands, over an array of test frequencies. It’s called by exact_fit() with the test frequencies equal to the band center frequencies, in order to create a matrix that represents the simultaneous equations relating the equalizer settings and the resultant gain.
It is also called with separate center frequency and test frequency arrays to generate the values for the frequency response plot. The number of response points calculated is essentially unlimited, though the result array or matrix needs to be appropriately dimensioned. The array of pointers indexing mode gives increased flexibility; when eq_resp() is called with rfmt=3, only the 0th row of the result array is actually accessed. This saves allocation space when the screen drawing routine calculates the response at say 275 different frequencies. In a system with 10 center frequencies, the fully allocated size of result[][] would be result[10][274]. But for frequency response use, only a pointer to an array pointer for a 275-entry vector needs to be set up and sent.
#define EXPORT __declspec(dllexport)
#include <math.h>
EXPORT
void eq_resp_r4(int ncf, double *cf, int gfmt, double *g, int dfmt, double *d, int ntf, double *tf, int rfmt, double **result)
{
/*
this version doesn't need +1 added to the loop termination condition
band-specific array index starts at 1; row 0 is used for overall response
int ncf number of center frequencies, indexed with i, first bracket, rows (transposed from Excel)
double *cf array of center frequencies
int gfmt format selector for use of g[]
double *g array of gain values
int dfmt format selector for use of d[]
double *d array of d values (denominator dissipation)
int ntf number of test frequencies, indexed with j; second bracket, columns (transposed from Excel)
double *tf array of test frequencies
int rfmt format selector for type of result
double **result 2D array of result values, pointer to array of pointers style
gfmt interpretation:
gfmt=0 means g[] is in dB
gfmt<>0 means g[] is the sqrt() of the desired band gain
currently we don't need any other configurations
dfmt interpretation:
dfmt=0 means ignore d[] and use default dissipation calc scheme as function of gain (return it in d[])
dfmt<>0 means d[] is the required denominator dissipation
currently we don't need any other configurations
rfmt interpretation:
rfmt=0: don't transpose; scale by log10(gain2)
rfmt=1: transpose: scale by log10(gain2)
(=1 mode is used by the ExactFit algorithm, which calls this function to get the response matrix)
rfmt=2: don't transpose: scale by 10.0; also write product to 0th row of the array
rfmt=3: only write product to 0th row of the array
(=3 mode is used by a calling function to get the overall system response)
*/
int i,j;
double gain2, sqrg, slimit, scale, ddiss, alpha, f, f2, num, den;
/* gain2 is the square of the gain, f2 is the square of relative frequency f */
/* num is used as a dummy to reduce storage */
/* important that this first row is initialized; used to pass a 1D result back */
for(j=1; j<=ntf; j++) {
result[0][j]=0.0;
}
slimit = 5.756E-6; /* matches oddset cell of 1E-4dB in Excel rev 0.9 */
alpha = 2.0;
for(i=1; i<=ncf; i++) {
/* loops across rows; first index; band center frequencies */
if (gfmt == 0) {
sqrg = pow(10.0,g[i]/40.0);
}
else {
sqrg = g[i];
}
if ( rfmt < 2 && sqrg-1.0 < slimit && 1.0-sqrg < slimit) {
sqrg = 1+slimit;
}
gain2 = sqrg*sqrg;
gain2 *= gain2;
if (rfmt < 2) {
scale = 1/log10(gain2);
}
else {
scale = 10.0;
}
if (dfmt == 0) {
if (i > 1) {
alpha = cf[i]/cf[i-1];
}
ddiss = (alpha - 1.0/alpha)/sqrg;
d[i] = ddiss;
}
else {
ddiss = d[i];
}
result[i][0] = 0.0;
for(j=1; j<=ntf; j++) {
/* loops across columns; second index; test frequencies */
f = tf[j]/cf[i];
f2 = f*f;
num = -1.0*f2*ddiss*ddiss;
den = (1.0-f2)*(1.0-f2)-num;
num -= gain2*num;
num = log10(1.0+num/den);
/* num now contains the Bel gain of the ith section at the jth frequency */
switch(rfmt) {
case 1:
result[j][i] = num * scale;
break;
case 0:
case 2:
result[i][j] = num * scale;
result[0][j] += 10.0*num;
result[i][0] += num;
break;
case 3:
default:
result[0][j] += 10.0*num;
break;
}
}
}
return;
}void klusolve(double **a, int n, double *b)
This routine solves a set of simultaneous equations; the LHS vector (the desired gain) is supplied in b[], and the routine overwrites this with the RHS solution vector (the settings needed to achieve it). The routine was assembled from two routines in the Numerical Recipes library. It performs an LU decomposition on the matrix a[][] (returning L and U packed into the original storage space, with the implicit unit diagonal omitted), then solves the associated simultaneous equations represented by the dot product of a and the vector b[] by back-substitution. The solutions are returned in vector b[]. This is license-free in any application where the routines are not separately accessible for general purpose use. See Numerical Recipes in C, 2nd Edition, pp 43-48.
#define EXPORT __declspec(dllexport)
#include <math.h>
#define NRANSI
#include "nrutil.h"
#define TINY 1.0e-20
/* both a and b are overwritten in this process */
EXPORT
void klusolve(double **a, int n, double *b)
{
int i,imax=0,j,k;
double big,dum,sum,temp;
double *vv;
int *indx;
int ii=0,ip;
/* vv=vector(1,n); */
/* choose vector() for single precision, dvector for double precision */
vv=dvector(1,n);
indx = ivector(1,n);
for (i=1;i<=n;i++) {
big=0.0;
for (j=1;j<=n;j++)
if ((temp=fabs(a[i][j])) > big) big=temp;
/* we'll trap for big ==0 singular matrix outside */
vv[i]=1.0/big;
}
for (j=1;j<=n;j++) {
for (i=1;i<j;i++) {
sum=a[i][j];
for (k=1;k<i;k++) sum -= a[i][k]*a[k][j];
a[i][j]=sum;
}
big=0.0;
/* imax = j;*/
/* should be unnecessary */
for (i=j;i<=n;i++) {
sum=a[i][j];
for (k=1;k<j;k++)
sum -= a[i][k]*a[k][j];
a[i][j]=sum;
if ( (dum=vv[i]*fabs(sum)) >= big) {
big=dum;
imax=i;
}
}
if (j != imax) {
for (k=1;k<=n;k++) {
dum=a[imax][k];
a[imax][k]=a[j][k];
a[j][k]=dum;
}
vv[imax]=vv[j];
}
indx[j]=imax;
if (a[j][j] == 0.0) a[j][j]=TINY;
if (j != n) {
dum=1.0/(a[j][j]);
for (i=j+1;i<=n;i++) a[i][j] *= dum;
}
}
for (i=1;i<=n;i++) {
ip=indx[i];
sum=b[ip];
b[ip]=b[i];
if (ii)
for (j=ii;j<=i-1;j++) sum -= a[i][j]*b[j]; /* = or not? */
else if (sum) ii=i;
b[i]=sum;
}
for (i=n;i>=1;i--) {
sum=b[i];
for (j=i+1;j<=n;j++) sum -= a[i][j]*b[j];
b[i]=sum/a[i][i];
}
/* free_vector(vv,1,n); */
/* choose free_vector() for single precision, free_dvector for double precision */
free_dvector(vv,1,n);
free_ivector(indx,1,n);
}
#undef TINY
#undef NRANSIvoid best_gain_r4(int nb, double *gin, double *gout)
This routine processes an array of gain values to determine if some gain normalization needs to take place in order to get the best performance out of the equalizer. The gain is entered as gin[] and the resultant output gout[] is fed to the ExactFit routine. gout[0] contains the additional gain that the equalizer needs to implement to get the overall response to where it needs to be. The equalizer should implement its own gain allocation rules for how this gain should be distributed.
#define EXPORT __declspec(dllexport)
#include <math.h>
#define grange 32
EXPORT
void best_gain_r4(int nb, double *gin, double *gout)
{
/* band gains use indices from 1, index zero is for gshift */
/* this ver doesn't need +1 on the loop termination */
int count[grange];
int i, igain, mostchans, mostgain;
double meangain = 0.0;
for(i=0; i<=grange; i++) {
count[i]=0;
}
for (i=1; i<=nb; i++) {
igain = grange/2 + (int) floor(gin[i]);
if (igain < 0) {
igain = 0;
}
if (igain > grange) {
igain = grange;
}
meangain += gin[i];
count[igain] += 1;
}
meangain /= (double) nb;
mostchans = 0;
mostgain = 0;
for (i=0; i<=grange; i++) {
if (count[i] > 0 && count[i] > mostchans) {
mostchans = count[i];
mostgain = i;
}
}
/* now mostgain is the most common gain value, biassed low */
/* note: to force flot, replace floor() with floorf() */
if (2*mostchans > nb) {
gout[0] = (double) floor((mostgain-grange/2));
}
else {
gout[0] = (double) floor(meangain);
}
for (i=1; i<=nb; i++) {
gout[i] = gin[i] - gout[0];
}
gout[0] += gin[0];
return;
}