Now Fix Those Drooping DAC and ADC Responses
In “Why does the frequency response of my DAC droop?”(which I’ll refer to here as ‘Part 1’) I asked the question:
Can the input path also cause droop that’s detectable when we analyze the data in the digital domain, without even going back to analog?
Let’s try to answer that here. If you are using a sampling ADC, the answer is generally “don’t worry”. Such an ADC takes a snapshot of the input signal over a brief “aperture” of time. This aperture is usually far narrower than the time between samples, so it has insignificant ‘smoothing’ effect on the frequency response.
However, if you are using the kind of delta-sigma ADC that is targeted at industrial instrumentation applications, you’ll probably get much more droop than you bargained for. (Do people actually bargain for droop? I suppose it’s just a figure of speech.)
The reason why delsig (to use the industry vernacular) ADCs have a droopy frequency response is that the usual averaging filters, used to smooth out the fast pulse streams from their front-end “modulators”, have analogous impulse responses to that of the zero‑order hold we just looked at. In fact, usually the droop in response is two to four times worse at any given frequency. This is because the filters used are usually, effectively at least, the cascade of two to four averaging filters.
In the case of the precision delsig ADC I’m most familiar with, the decimation filter has four stages and therefore has a sinc4() response. At any given signal frequency it therefore has four times (expressed in dB), the droop shown in figure 1 of . In other words, it’s ‑12 dB at 0.443 times Fs. Such a gross departure from flatness of frequency response is not of consequence when what you really want is just the weight of bananas on a scale. But for most audio, communications and vibration measurement systems, it’s just plain terrible. And that’s before you add on the extra droop you’ll get if you feed the digital signal into a DAC.
There’s a good side to this response effect though. Figure 1 of Part 1 showed that the sinc() response “bounces back up” to only about ‑13.3 dB at about 1.43 times Fs. This is a reminder that the simple averager is not a very good filter for getting rid of high frequency variations. But if you put four of them in series to get sinc4(), you now have a stopband response that only bounces back to around ‑53 dB, shown in figure 1 of this piece. That’s quite useful filtering, usually more than enough for precision measurements in the time domain where there’s not too much high frequency interference. But the passband response is now way ‘soggier’ than flat. What can we do about this? This is a Filter Wizard piece, so you just know that filters are going to be involved in the remedy for this response droop. And in the ADC case, a filter was the cause of it in the first place!
Figure 1: The sinc4() response of the PSoC3 ADC’s decimation filter.
You might have a system that suffers from both types of droop when measured from input to output (i.e. a droopy ADC and a droopy DAC). You might be tempted to apply one fix for both. But I recommend that you treat the input side and the output side separately. That’s because your data acquisition system probably shares data with other systems and analysis computers, so you want both the ‘record’ and ‘replay’ processes to be correct.
I’ll assume from now on that you do have a droop problem on one or both ends. If you don’t, it’s either because you already recognized the issue and fixed it, or you used components (for instance, audio-grade converters) that didn’t suffer from the issue in the first place.
Let’s look at the DAC side of things first. In a typical data ‘replay’ path, your data might pass through a digital filter on the way to the DAC. It might also go through an analog ‘reconstruction’ filter after conversion, before it reaches the final output of the system. If you have neither an analogue nor a digital filter in your system (harrumph! Why?), and you’re suffering from droop, then you will need to add something extra to your system. But if there is a filter in the signal path, the chances are that it can be altered to compensate for the droop.
I’ll start with the case that I’m not going to cover here (if that makes sense). If you only have an analog filter, it will need to be redesigned to have a different, rising frequency response. Whether this can be done, and how to do it if it is possible, is just too complicated to go into here (a case where this was done is referred to in passing in “When the mask slips…”). In the “good old days” I designed many reconstruction filters with a peaked response to correct for a DAC’s sinc() droop, while still suppressing the ‘images’ from the sampling process. Rather than using tables or coefficient equations, the design usually requires careful ‘fitting’ of the response with a dedicated computer program.
Incidentally, on a historical note, modern active filter design was heavily driven in the 1960s and 1970s by the needs of the telephone industry, which was making a transition to digital telephony at the still-standard sample rate of 8 ksps. The highest required audio frequency was 3.4 kHz, which makes the frequency of the lowest sampling image (images are the additional high frequency components that appear in the reconstructed output signal) equal to 4.6 kHz, which is only a factor of 1.35 away. Separating these two frequencies requires fairly sharp filtering, and this was typically done using active elliptic lowpass filters. Had they chosen a higher sample rate for digital telephony, the filtering requirements would have been alleviated, and much less effort would have gone into active filter design methodologies. The need for Filter Wizards would have been reduced, and I might have ended up doing something completely different!
OK, nostalgic waffle mode off, let’s look at what I can contribute to droop management on the replay side without tweaking the analogue filtering. The key question: is there a digital filter in your signal path? The digital filter might be implemented in dedicated hardware, or might be buried in the code that creates or massages the data that you’re reproducing.
No digital filter hardware? Then here’s the easiest way to fix things up. You can add a very simple digital filter – so simple that it can be done in software – that can give a very good correction of sinc() droop up to a useful fraction of the sample rate. It’s the simplest case of what I call the “zero-adding” method. You might recall from the discussion in “Now Synthesize Your Filters Using High-school Algebra” that a ‘zero pair’ can be expressed as a second-order polynomial in the unit delay variable z-1. The effect that this small filter has on a system’s frequency response depends on the coefficients. In those FIR articles I looked at using them to produce deep nulls in the stopband. Here we’ll use just one zero pair (giving a second-order polynomial) to provide a gentle boost to the passband frequency response, without doing significant harm anywhere else.
Table 1: z-1 coefficients for the “zero-adding” method.
Table 1 contains all you’re likely to need (all thanks to the “Million Monkeys” – that terminology will become clear in a forthcoming post). It gives the coefficient K of the z-1 term in the added second order polynomial when the constant and z-2 terms are equal to ‑1. To leave the overall gain unaffected we need to scale all the coefficients by 1/(K-2). So the added term has the form:
with positive K as given in the table. The table also shows the peak dB error to expect for input frequencies up to the column limit frequency.
To use the method, first decide the fraction of the data sampling frequency up to which you’d like to fix up the droop, then pick the column in table 1 with the next-higher value. The row you’ll use for regular DAC droop correction is the sinc1 row. The accuracy of the correction falls as the fractional frequency range rises. For sinc1, table 1 extends to Fs/3. You really shouldn’t be expecting an otherwise-unfiltered system to be functional at higher frequencies than that – it’s too close to the sampling frequency and you will be getting significant amounts of image frequency in your output signal.
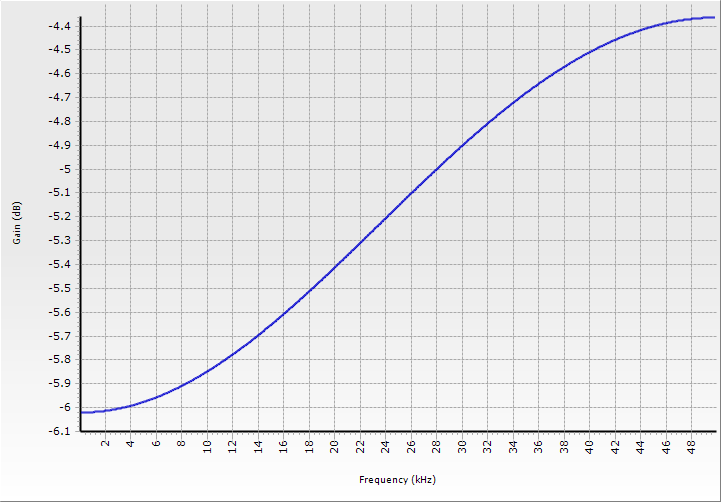
Let’s say your sample rate is 100 ksps and you want a good flat frequency response up to 20 kHz, which is Fs/5. Choose the Fs/4 column and the sinc1 row of table 1, then read out K = 21.04096. Calculating the coefficients in [1] gives the filter calculation you need to do for the i-th sample, whether in hardware or in the software flow, as:
output(i) = -0.05252*input(i) + 1.10504*input(i-1) -0.05252*input(i-2) [2]
If there’s already a gain scaling operation in your system, you can roll equation [1]’s constant factor of (K-2) into that calculation instead. Table 1 indicates that the worst-case approximation error in this case is ±0.045 dB up to Fs/4, so this is a pretty good fix for the droop. The frequency response of [2] right up to Nyquist is shown in figure 2. It continues to boost at frequencies above 20 kHz, but not excessively.
Figure 2: Frequency response of ‑0.5252 + 1.10504z-1 ‑ 0.5252z-2.
If there is a digital filter in your system and you nevertheless still have a droop issue, then it’s finger-wagging time for someone. The most common function for such a filter is to help out with interpolating or ‘upsampling’ your replay data so that you can apply it at a higher sample rate to the physical DAC. One reason why you do this is to mitigate the droop problem in the first place! So someone should have fixed it already...
If your digital filter implementation allows you to add an extra zero pair to the transfer function, just use the method described above. The addition is straightforward when you’re using an FIR filter; it increases the tap count by two. If you know the existing coefficients, a simple spreadsheet calculation can do the multiplication needed to get the new coefficients.
If you’re using an IIR filter architecture and can add another biquad, you just use the polynomial created above as the numerator, then define a do-nothing denominator (with the z-1 and z-2 terms both zero). A slight waste of computing cycles but it will work fine. You can also use the zero-adding method if you can see that one of the numerators in your IIR filter only has one term, in which case you just discard it and add the new zero pair.
If you are using an IIR filter and can change the coefficients but not the order of the filter (i.e. the number of biquads) then you need a slightly different method, the “zero-shifting” method. Instead of just adding a zero pair with the right amount of boosting frequency response, the zero-shifting method removes an existing zero pair, replacing it with one that has less droop. The effect of this is to boost the frequency response without changing the filter order.
Table 2: z-1 multiplying factors for the zero-shifting method.
The zero-shifting method could work in principle with any choice of initial zero pair. To simplify matters and permit the use of another precalculated table, the approach given here assumes you can find and remove a zero pair at Nyquist. In an IIR filter, such a pair is the result of the bilinear transform acting on a pair of s-plane zeroes at infinity (sorry for the sudden burst of filter jargon!). It’s very unusual to find a workable IIR transfer function that doesn’t have at least one of these as a biquad numerator.
For instance, this is the case for nearly all the lowpass and bandpass IIR filters produced by code that uses the standard Bilinear Transform method to create its IIR functions. The only exceptions are first-order lowpass and second-order bandpass filters. If you study the numerators of most other lowpass or bandpass filter functions from such filtering packages, you’ll find that at least one of them will be have the form (C + 2Cz-1 + Cz-2) where C is a constant (often unity).
The compensation method here involves changing just one of these terms to be (C + C*(pick a K from table 2)*z-1 + Cz-2). I could hardly have made it easier for you; you just have to change one coefficient in your factorized transfer function. If you can arrange it, I think it’s a good idea to start with a transfer function that has at least two zero pairs at Nyquist. This will help to preserve good stopband rejection.
Adjusting coefficients in this way increases the DC gain of the filter (it’s proportional to the sum of the numerator coefficients). To get back to the original gain, you’ll need an extra scaling factor of 2/(K+1), which you can either multiply into one of the numerators or into your overall system gain constant.
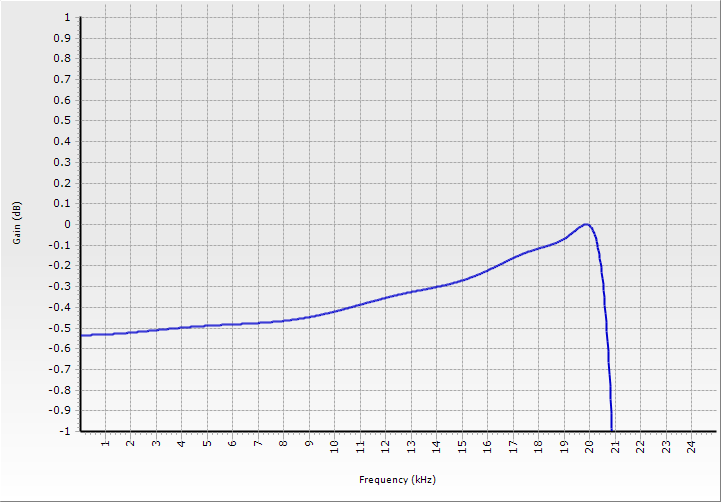
Using the same frequency example as before, let’s now assume that you initially have a nice flat passband 0.02 dB ripple eighth-order Chebyshev filter in the system, cutting off at 20 kHz. The passband response of that filter is shown in figure 3. The coefficients of the four biquad sections (the unity z0 coefficient in the denominator is not shown in this format) are:
The first three numbers of each quintuplet are the numerator coefficients, and you can see that in this case they all follow the (C + 2Cz-1 + Cz-2) pattern. If we go to table 2 and find the intersection of the sinc1 row and the Fs/4 column, it tells us to multiply one of the z-1 coefficients – it doesn’t matter which one – by K = 1.269685. Doing this results in the response (after gain correction) shown in figure 4. This highlights an important issue, namely that by raising the gain of the filter at some frequencies, we run the risk of premature overload as the digital path clips early. The droop caused by the zero‑order hold at the output of a DAC is ‘real’ attenuation, and you need to feed a larger digital signal into the DAC in order to get a given magnitude of sinewave component out. This takes us into the realm of digital filter overload, which is a great subject for a whole Filter Wizard in itself, duly noted...
Figure 3: The (flat) frequency response of the n=8 Chebyshev lowpass filter.
Figure 4: Response of figure 3’s filter with zero-shifting sinc1() compensation.
The stopband rejection of figure 4’s filter is not significantly degraded. That’s because the original Chebyshev filter had all four zero pairs at Nyquist, and we only shifted one of them.
Incidentally both the zero-adding and zero-shifting methods are linear phase, when implemented as described here. Changing the numerator with the zero-shifting method doesn’t change the filter’s group delay at all. The zero-adding method increases the group delay by exactly one sample time.
What if instead of an IIR-based filter, you have an FIR filter that already has the maximum number of taps that your hardware or firmware can cope with, and your really can’t stretch it by another two to use the zero-adding method? If you have access to a suitable ‘ordinary’ FIR filter design program, one approach is to design a new starting filter with a reduced tap count (by two or more) compared to your present filter. If this can still meet all the passband and stopband requirements you originally had, use this as your new starting point and apply the zero-adding method as described previously. Some filter design programs will even do the droop compensation for you – but I insist that you at least try to do it once yourself before you click that box!
The toughest gig is when you have the coefficients, but no access to the design methodology that produced them. If you need to keep the tap count the same but change the existing response slightly to rectify a droop issue, you will have to roll your sleeves up and do it the hard way. In “Analyze FIR filters using just High-school Algebra” we saw how an FIR coefficient set can be treated as a polynomial whose roots can be found, and the zero pair factors calculated from them. That’s what you’d do here. Paste the filter coefficients into a root-finder program or spreadsheet (such as this) and find the roots.
If you find a pair of zeroes very close to Nyquist (a pair of roots with a value very close to ‑1), then you can use the zero-shifting method “as-is”. If so, replace them by the polynomial for the new, shifted zero pair (you don’t need to know the roots of that), and multiply everything back up to get a new set of coefficients. If there are no zero pairs very close to Nyquist, there is a technique that can modify the filter you’ve got in order to force this. It’s all rather long-winded so I won’t give an example here.
What about the ADC side of things? The main difference compared to the DAC case is that a droopy delta-sigma ADC usually has a response with a higher power of sinc(). That’s why tables 1 and 2 run right up to sinc5().
Feeling Active? Don’t be tempted to correct the droop of a delta-sigma ADC by using a ‘peaking’ analog filter in front of the ADC. This will give you horrible overload problems and will further degrade the aliasing tendency of the sinc() decimator. It will be hard to design and may well spoil your system’s offset and noise performance too. I hope you understand how hard it is for me to advise you not to use an analog filter, but there it is!
Correcting the ADC droop digitally proceeds in the same way as for the DAC compensation, and both the zero-adding and the zero-shifting methods can be employed. Now, if you have significant droop, chances are you have a sincn()-responding decimator. That will cause some aliasing, which is bad news in frequency domain applications. If you want to use an instrumentation-grade delta-sigma ADC for audio or other frequency domain applications, you really ought to have a better grade of decimation filter designed into your system, then run the ADC at say 2x or 4x the desired output sampling rate. This is typical within audio-grade ADCs.
If you really can’t afford to change the system sample rate but do need that flatter frequency response, you can use the zero-adding method to build a response compensator as shown for the DAC case. It’s really not the optimum solution, though, it’s just a Band-Aid, as my US friends would call it. For higher powers of sinc(), a single section doesn’t provide particularly accurate correction; up to Fs/4, it’s accurate to a bit more than a quarter of a dB. Higher-order correction filters will do a better job.
The zero-adding method also works fine for ADC use. Reading along the sinc4 row of table 2, in the Fs/4 column we find K = 3.42206. If we take the Chebyshev filter example of figure 1 and multiply one of its numerator z-1 coefficients by 3.42206, we get the response shown in figure 5 (with the gain adjusted so that the peak is at 0 dB).
Figure 5: Response of figure 3’s filter with zero-shifting sinc4() compensation.
With luck, this article and its prequel have given you a picture of where response droop comes from and how you can make it go away. These simple techniques can often save you from having to do battle with a full-blown filter design. They also give an insight into what the intricate moving parts of a transfer function can be made to achieve. So, filter fans, lift up your responses with a little snap of polynomial magic. Don’t let droop spoil your day. And I mean that most sinc-erely…!